No ei se energia mystisesti sinne vaunuunkaan siirry sisälle. Onko käsite kimpoaminen tuttu?
Basic physical principles of deflection
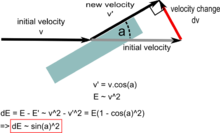
Very simple physical model of the slope effect. Kinetic energy absorbed by armour is proportional to the square of the sine of angle (maximal for 90°). Friction and deformation of target are neglected
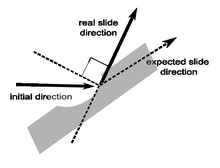
How a groove caused by projectile impact increases the effective incident angle (lower slope effect)
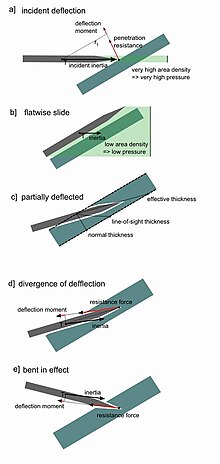
Illustration of some possible effects that can occur when a projectile impacts sloped armour
The behaviour of a real world projectile, and the armour plate it hits, depends on many effects and mechanisms, involving their material structure and
continuum mechanics which are very difficult to predict. Using only a few basic principles will therefore not result in a model that is a good description of the full range of possible outcomes. However, in many conditions most of these factors have only a negligible effect while a few of them dominate the equation. Therefore a very simplified model can be created providing a general idea and understanding of the basic physical principles behind these aspects of sloped armour design.
If the projectile travels very fast, and thus is in a state of
hypervelocity, the strength of the armour material becomes negligible – as by the impact both projectile and armour will melt and behave like
fluids – and only its area density is an important factor. In this limiting case the projectile after the hit continues to penetrate until it has stopped transferring its
momentum to the target matter. In this ideal case only momentum, area cross section, density and LOS-thickness are relevant. The situation of the penetrating metal jet caused by the explosion of the
shaped charge of
HEAT ammunition, forms a good approximation of this ideal. Therefore, if the angle is not too extreme, and the projectile is very dense and fast, sloping has little effect and no relevant deflection takes place.
On the other extreme, the more light and slow a projectile is, the more relevant sloping becomes. Typical World War II Armoured Piercing shells were bullet-shaped and had a much lower velocity than a shaped charge jet. An impact would not result in a complete melting of projectile and armour. In this condition the strength of the armour material becomes a relevant factor. If the projectile would be very light and slow, the strength of the armour might even cause the hit to result in just an
elastic deformation, the projectile being defeated without damage to the target. Sloping will mean the projectile will have to attain a higher velocity to defeat the armour, because on impact on a sloped armour not all kinetic energy is transferred to the target, the ratio depending on the slope angle. The projectile in a process of
elastic collision deflects at an angle of 2
(where
denotes the angle between the armour plate surface and the projectile's initial direction), however the change of direction could be virtually divided into a
deceleration part, when the projectile is halted when moving in a direction perpendicular to the plate (and will move along the plate after having been deflected at an angle of about
), and a process of elastic acceleration, when the projectile accelerates out of the plate (velocity along the plate is considered as invariant because of negligible friction). Thus the maximum energy accumulated by the plate can be calculated from the deceleration phase of the collision event.
Under the assumption that only elastic deformation takes place and that the target is solid, while disregarding
friction, it is easy to calculate the proportion of energy absorbed by the target if it is hit by projectile, which, if we also disregard more complex deflection effects, after impact bounces off (elastic case) or slides along (idealised inelastic case) the armour plate.
In this very simple model the portion of the energy projected to the target depends on the angle of slope:
where
- : Energy transferred to the target
- : Incident kinetic energy of projectile
- : Angle of the sloped armour plate from the projectile's initial direction
However, in practice the AP-shells were powerful enough that the forces involved reach the
plastic deformation limit and the elasticity of the plate could accumulate only a small part of the energy. In that case the armour plate would yield and much of the energy and force be spent by the deformation. As such this means that approximately half the deflection can be assumed (just
rather than 2
) and the projectile will groove into the plate before it slides along, rather than bounce off. Plasticity surface friction is also very low in comparison to the plastic deformation energy and can be neglected. This implies that the formula above is principally valid also for the plastic deformation case, but because of the gauge grooved into the plate a larger surface angle
should be taken into account.
Not only would this imply that the energy transferred to the target would thus be used to damage it; it would also mean that this energy would be higher because the effective angle
in the formula is now higher than the angle of the armour slope. The value of the appropriate real
' which should be substituted cannot be derived from this simple principle and can only be determined by a more sophisticated model or simulation.
On the other hand, that very same deformation will also cause, in combination with the armour plate slope, an effect that diminishes armour penetration. Though the deflection is under conditions of plastic deformation smaller, it will nevertheless change the course of the grooving projectile which again will result in an increase of the angle between the new armour surface and the projectile's initial direction. Thus the projectile has to work itself through more armour and, though in absolute terms thereby more energy could be absorbed by the target, it is more easily defeated, the process ideally ending in a complete ricochet.
http://en.wikipedia.org/wiki/Sloped_armour










